I have proposed an experiment to test the ideas discussed in the previous pages. The details of my proposed experiment can be found in this published paper, or in this preprint. An earlier version of the experiment (published in 2008) can be found in this preprint, and a simplified summary or a “proof of concept” can be found in this preprint (published in 2015).
The central goal of the proposed experiment is to test the hypothesis that quantum correlations are a consequence of—or a measure of—the torsion at each point in our physical space:
This upper bound is derived in the last appendix of this paper (see also this paper). The experiment can be performed either in the outer space or in a terrestrial laboratory. In the latter case the effects of gravity and air resistance would complicate matters, but it may be possible to choose experimental parameters carefully enough to compensate for such effects.
With this assumption, consider a “bomb” made out of a hollow toy ball of diameter, say, three centimeters. The thin hemispherical shells of uniform density that make up the ball are snapped together at their rims in such a manner that a slight increase in temperature would pop the ball open into its two constituents with considerable force. A small lump of density much greater than the density of the ball is attached on the inner surface of each shell at a random location, so that, when the ball pops open, not only would the two shells propagate with equal and opposite linear momenta orthogonal to their common plane, but would also rotate with equal and opposite spin momenta about a random axis in space. The volume of the attached lumps can be as small as a cubic millimeter, whereas their mass can be comparable to the mass of the ball. This will facilitate some possible spin directions for the two shells, whose outer surfaces can be decorated with colors to make their rotations easily detectable.
Now consider a large ensemble of such balls, identical in every respect except for the relative locations of the two lumps (affixed randomly on the inner surface of each shell). The balls are then placed over a heater—one at a time—at the center of the experimental setup, with the common plane of their shells held perpendicular to the horizontal direction of the setup. Although initially at rest, a slight increase in temperature of each ball will eventually eject its two shells towards the observation stations, situated at a chosen distance in the mutually opposite directions. Instead of selecting the directions and
for observing spin components, however, one or more contact-less rotational motion sensors—capable of determining the precise direction of rotation—are placed near each of the two stations, interfaced with a computer. These sensors will determine the exact direction of the spin angular momentum
(or
) for each shell in a given explosion, without disturbing them otherwise so that their total angular momentum would remain zero, at a designated distance from the center. The two interfaced computers can then record this data entirely locally, in the form of a 3-dimensional map of all such directions, at each observation station.
Once the actual directions of the angular momenta for a large ensemble of shells on both sides are fully recorded, the two computers are instructed to randomly choose a pair of reference directions, say for one station and
for the other station—from the two 3-dimensional maps of already existing data—and then calculate the corresponding pair of numbers
and
. The correlation function for the bomb fragments can then be calculated as
with
where n is the number of experiments performed. According to Bell’s reasoning [which amounts to setting in Eq. (1)] the calculation done in Eq. (2) would not yield correlation stronger than
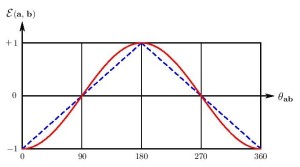
where is the angle between the vectors
and
. On the other hand, if my reasoning is correct and quantum correlations are indeed a consequence of the torsion in our physical space as I have hypothesized [cf. equation (1) above], then we expect the correlation function (2) to yield
The plot below shows the difference between the correlations predicted by functions (4) and (5):
Undoubtedly, there would be many different sources of errors in a macroscopic experiment of this nature. However, at least according to David Wineland the proposed experiment is “doable.”
PS: I have recently won the 10,000 Euros offered by Richard Gill for theoretically producing the 2n angular momentum vectors, and
, appearing in the above equations. He had foolishly claimed that it was mathematically impossible to construct such 2n vectors and had challenged me to produce them as a “proof of concept” for my proposed experiment. I defeated his challenge in May and June of 2014 by explicitly producing the 2n vectors in these four simulations: (1), (2), (3), and (4), which reproduce the strong correlations purely local-realistically. This suggests that my proposed experiment will be a spectacular success. It will reproduce the strong correlations exactly as I have predicted in several of my papers, for example in Appendix C of this paper where I have given a proof of the strong correlation.
PPS: In the above experiment I have used two hemispheres of an “exploding” ball as a convenient means to illustrate the physical scenario. But in practice a spherically asymmetric hemisphere would wobble violently because of all sorts of inertial effects. A much better system would be something like two flexible squashy balls, squeezed together initially, and then released as if they were parts of a single bomb. This will retain the spherical symmetry of the two constituents after the “explosion” and reduce the inertial effects to near zero. For this system, however, it may be harder to maintain the singlet nature of the composite system (i.e., to maintain the vanishing total spin angular momentum of the composite system).
PPPS: In the published version of the paper the following two paragraphs have been added: 
PPPPS: With the bomb made out of two squashy balls (instead of a single ball) which rapidly reshape to perfectly round spheres, the determination of spin directions would be easier, since the spin and rotation axes for each sphere would then be the same. It would still be important to eliminate aerodynamic effects before the final shapes are stabilized. A good quality check of the setup would be to compare how accurately the spins are anti-parallel, thus making sure that the singlet property for each pair of the measured spins is maintained.






Hi Joy,
Wow! Very nice blog space here! I am not sure if I told you this before but I thought of another possibly doable macroscopic experiment. It is fairly simple thought-wise so here we go. You should be able to have someone do an experiment similar to Weihs, et al but instead of trying to count single photons, you would count a macroscopic bunch of identical in phase photons say like 10K of them. With proper filtering techniques, I think this experiment could probably be done. If the measured correlations exceed the CHSH inequality then you have macroscopic validation that Bell was wrong since the “bunches” of photons are really just a special macroscopic EM pulse.
I am not sure if I told you this before but I thought of another possibly doable macroscopic experiment. It is fairly simple thought-wise so here we go. You should be able to have someone do an experiment similar to Weihs, et al but instead of trying to count single photons, you would count a macroscopic bunch of identical in phase photons say like 10K of them. With proper filtering techniques, I think this experiment could probably be done. If the measured correlations exceed the CHSH inequality then you have macroscopic validation that Bell was wrong since the “bunches” of photons are really just a special macroscopic EM pulse.
Now, you might be asking how do we figure out what the E field value might be for 10K photons or how do we know when we have about 10K photons? I have derived a simple equation to figure that out in CGS units.
Where n = 10K identical in phase photons and lambda = 700nm wavelength. Well, perhaps we don’t need as many as 10K photons but that value for the E field strength is what we would be looking for at the detector for 10K. Of course it would be reduced by the filters, etc. but that should be able to be determined.
Perhaps you might want to run this scenario by Gregor Weihs and see if he thinks it could be done? Please ask if any questions.
Best,
Fred
Hi Fred,
Thank you for your interesting proposal. Let me see if I understand your idea correctly. We begin by preparing a sufficiently large number of “identical in phase” photons so that they can be characterized by the same initial state. It is important for the photons to be in the same initial state, because what we are looking for is correlations between the values of the E-field strength that are determined by the same initial state. Assuming that this can be done (which is a very big assumption), how do we then observe coincidences between such values? As we know, in the experiment by Weihs et al. they observed coincidences between polarizations of a single pair of photons. Detections of remote polarizations were said by them to be “coincident” if they occurred within a given time window. Are you saying that in your proposal we should look for such coincidences between the values of the E-field strength? I think that would be a very difficult thing to observe, even if we ignored the inevitable smearing in the values because of the time window. It seems to me that strong correlations would be simply averaged out because of the smearing.
On the theoretical side, it is not clear to me how such values in the E-field strength would depend on the torsion within the 3-sphere. According to my model if torsion does not play a significant role in the experiment then there will be no violation of Bell inequality.
So there is much to think about in your proposal. But it is an interesting idea nevertheless.
Best,
Joy
Hi Joy,
I am assuming that the parametric down conversion of the laser would take care of the initial state problem. Of course a stronger laser may be required. Then some kind of filter on each beam to make sure we have mostly identical inphase photons in each beam. The detectors would be detecting a certain E field value level. IOW, referring to the Weihs, et al, experiment, a detection would be a + 1 if the E field value was high enough, and -1 if low enough or zero. The polarization filters that are randomly rotated are either going to be blocking the signal or not, basically. So if this scenario can beat the CHSH inequality on coincidences, then you will have some validation that Bell was wrong. Of course the devil is in the actual details of trying to perform this experiment.
For the timing thing, the laser would have to be pulsed somehow so that we have EM pulses hitting the down convertor. And I suppose that timing need be taken into consideration of lining up the detections. But these “special” EM pulses are going to be macroscopic spinors so the torsion of the 3-sphere topology should apply I would think. I suppose only an experiment will tell though.
Best,
Fred
Hi Fred,
I understand the experiment better now.
Suppose we do the experiment and observe violations of the CHSH inequality. Would the diehard believers in non-locality be convinced by the experiment? I bet they would say: This is no surprise. The experiment only confirms Bell’s theorem, because the E field generated by the large number of photons can be easily described by QED. It is therefore no surprise that CHSH inequality is violated.
I am of course being a devil’s advocate, but how would you answer such a charge?
Put differently, how can you be sure that the “special” EM pulses are macroscopic spinors?
Best,
Joy
Hi Joy,
Of course the diehards would want to claim that the experiment is still “quantum” somehow. But we are not detecting single photons; we are detecting a macroscopic EM signal. If it beats CHSH, then that would be good enough for me of a macroscopic test and hopefully a bunch of others that aren’t diehards. I doubt if diehard Bell believers will ever change their position. As we have well seen these past years. Even if your mechanical experimental test beat Bell, they still wouldn’t accept it. But hopefully reasonable people would.
Best,
Fred
Hi Fred,
Yes, it would be good enough for me too.
There is, however, an advantage in the mechanical experiment. There is no way to fit quantum entanglement into it. The exploding bomb is obviously in a product state, not in an entangled state. I think most physicist would then accept that strong correlations are not exclusive to quantum entanglement.
Best,
Joy
Hi Joy,
A correction on my equation above; that should be E_o for the electric field and plugged into the wave equation of course.
That is true what you say about the mechanical experiment. It actually does two things.
Best,
Fred
Hi Joy,
What I wrote above does not work because there will be a racemic mix of spin 1 and -1 photons coming from the laser in each EM pulse. So a different way has to be devised to get the identical photon bunches in the two beams.
Best,
Fred
Hi Joy,
Thought about this some more. It is clear that for a macroscopic EM test, we have to simulate the singlet state somehow. Which shouldn’t be too hard to accomplish since if one beam to detector A is + 1 spin then the other to detector B has to be -1 spin and the other way around. The experiment would have to have two synchronized lasers with some kind of filters that would produce +1 spin in one beam and -1 spin in the other. Then a random optical switching device to provide the filtered EM pulses to the detector paths. I think this works as a thought experiment but perhaps a clever experimenter some day could make it a reality.
Best,
Fred
Hi Fred,
Thanks for your further thoughts. I will ask one of my friends about your proposal. He is a well known laser expert. I might be able to persuade him to read your comments.
Best,
Joy
Hi Fred, Joy,
Fred I haven’t had time to study all of your comments, but I have recently been working hard to better understand how Maxwell’s theory and Quantum theory come together best. I’m glad you’re actively thinking along those lines too. I’m not sure I understand exactly what you’re proposing, but it seems that you’re saying “the detectors would be detecting a certain E field value level (or E field strength).” I’ve spent the last few days reading Harry Paul’s “Intro to Quantum Optics”, and he states on page 41: “…it is impossible – due to the enormously high frequency of light — to measure the electric field strength.” What is detected is the energy transfer (~E^2) from the radiation field to the atomic receiver. Again, p. 21, “the electric field strength is not directly observable in the optical domain.” What is observable is the intensity. You can think of this like probability amplitude and probability. Remember that what the detectors are doing is being excited to new energy levels (or ionized) and that’s all! You may be suggesting that the E-field can be inferred, I’m not sure.
Paul’s book is a very good one (written by an experimentalist, who says: “The ‘photons of a theoretician’, as we might call them, are not at all the same thing as those described by an experimentalist who reports that a photon was absorbed at a particular position by a detector.” He is obviously very good on describing experiments, but also good on both classical and quantum optics. I recommend it.
By the way, Jonathan Dickau started a thread on FQXi about some work of Steven Kenneth Kauffmann on self-gravitational upper bounds on localized energy. In looking thru his papers (on arXiv and viXra) I found that he has some fascinating ideas, so I’m recommending his work to those who appreciate (good) new ideas.
Ed
Hi Edwin,
Yes, the electric field strength would be inferred from the square of the field strength = energy density. I mainly just presented my E_o equation above that I derived so that we have some idea about the number of identical inphase photons involved in the signal. Really, the detectors are going to either detect a signal or not detect a signal depending on the alignment of the random positions of the polarizers, etc. With 10K identical photons at 700nm wavelength, we have about 0.05 joules/cm^3 energy density. That seems high so maybe we don’t need that many photons. Probably 1K photons would do it and still is plenty macroscopic enough. I wonder what power for a laser that would require?
I will look into the book you mention above. It is obvious for sure that there is a difference between theoretical photons and experimental photons after reading a few optical experiment papers.
Yes, I made a note on Jonathan’s FQXi thread about Christoph Schiller’s work on maximum force. Kauffmann seems to have rediscovered what Schiller presented a few yeares ago and perhaps went a bit further with it. Schiller’s derivation of Einstein’s field equation (GR) starting from the concept of maximum force is pretty remarkable though.
Best,
Fred
An experiment with classical optical field has been done, and published in an optics journal: https://www.osapublishing.org/optica/abstract.cfm?URI=optica-2-7-611
It seems to be similar to the type of experiment Fred has been suggesting above.