Topologies of the 3- and 7-spheres

Check out also the Hopf Fibrations of $S^{15}$ discussed in the video: Sedenion and Sons!

S^3 is S^2 worth of circles. Each circle S^1 in S^3 can be mapped to a point in the base space S^2 by this Hopf map.

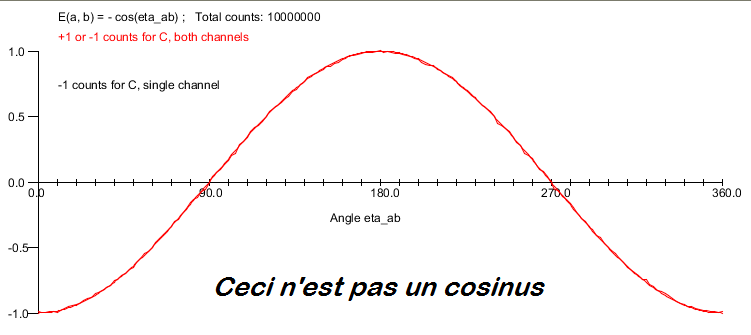
My paper based on these concepts refuting Bell’s theorem can be found here: Symmetric

Local Causality and the Division Algebras:

In previous pages I have sketched the crucial role played by the 3- and 7-dimensional spheres in understanding the existence of quantum correlations. What is so special about 3 and 7 dimensions? Why is the vector cross product definable only in 3 and 7 dimensions and no other? Why are ${{\mathbb R}}$ , ${{\mathbb C}}$ , ${{\mathbb H}}$ , and ${{\mathbb O}}$ the only possible normed division algebras? Why are only the 3- and 7-dimensional spheres nontrivially parallelizable out of infinitely many possible spheres? Why is it possible to derive all quantum correlations as local-realistic correlations among the points of only the 7-sphere?

The answers to all of these questions are intimately connected to the notion of factorizability introduced by Bell within the context of his theorem. Mathematicians have long been asking: When is a product of two squares itself a square: ${{x^2\,y^2 = z^2\,}}$ ? If the number ${{z}}$ is factorizable, then it can be written as a product of two other numbers, $z=x\,y$ , and then the above equality is seen to hold for the numbers $x$ , $y$ , and $z$ . For ordinary numbers this is easy to check. The number 8 can be factorized into a product of 2 and 4, and we then have ${{64 = 8^2 = (2 \times 4)^2 = 2^2\times 4^2 = 64}}$ . But what about sums of squares? A more profound equality holds, in fact, for a sum of two squares times a sum of two squares as a third sum of two squares:

$\displaystyle (x_1^2 + x_2^2)\,(y_1^2 + y_2^2) \,=\, (x_1^{}y^{}_1 - x^{}_2y^{}_2)^2 + (x^{}_1y^{}_2 + x^{}_2y^{}_1)^2\,=\,z_1^2 + z_2^2. \ \ \ \ \ \ \ (1)$

There is also an identity like this one for the sums of four squares. It was first discovered by Euler, and then rediscovered and popularized by Hamilton in the 19th century through his work on quaternions. It is also known that Graves and Cayley independently discovered a similar identity for the sums of eight squares. This naturally leads to the question of whether the product of two sums of squares of ${{n}}$ different numbers can be a sum of ${{n}}$ different squares? In other words, does the following equality hold in general for any ${{n}}$ ?

$\displaystyle (x_1^2 + x_2^2 + \dots + x_n^2)\,(y_1^2 + y_2^2 + \dots + y_n^2) \,=\, z_1^2 + z_2^2 + \dots + z_n^2. \ \ \ \ \ \ \ (2)$

As I noted on this page, it turns out that this equality holds only for ${{n}}$ = 1, 2, 4, and 8. This was proved by Hurwitz in 1898. It reveals a deep and surprising fact about the world we live in. Much of what we see around us, from elementary particles to distant galaxies, is an inevitable consequence of this simple mathematical fact. The world is the way it is because the above equality holds only for ${{n}}$ = 1, 2, 4, and 8. For example, the above identity is equivalent to the existence of a division algebra of dimension ${{n}}$ over the field ${{\mathbb R}}$ of real numbers. Indeed, if we define vectors ${{{\bf x}=(x_1,\dots, x_n)}}$ , ${{{\bf y}=(y_1,\dots, y_n)}}$ , and ${\bf z}={\bf x}*{\bf y}$ in ${{{\mathbb R}^n}}$ such that $z_i$ are functions of $x_j$ and $y_k$ determined by equation (2), then

$\displaystyle ||{\bf x}||\,||{\bf y}|| \,=\, ||{\bf x}*{\bf y}||\,. \ \ \ \ \ \ \ (3)$

Thus the division algebras ${{\mathbb R}}$ (real), ${{\mathbb C}}$ (complex), ${{\mathbb H}}$ (quaternion), and ${{\mathbb O}}$ (octonion) we use in much of our science are intimately related to the dimensions ${{n}}$ = 1, 2, 4, and 8. Moreover, from the equation of a unit sphere,

$\displaystyle x_1^2 + x_2^2 + \dots + x_n^2 \,=\,1\,, \ \ \ \ \ \ \ (4)$

it is easy to see that the four parallelizable spheres ${{S^0}}$ , ${{S^1}}$ , ${{S^3}}$ , and ${{S^7}}$ correspond to ${{n}}$ = 1, 2, 4, and 8, which are the dimensions of the respective embedding spaces of these four spheres. What is not so easy to see, however, is the fact that there is a deep connection between Hurwitz’s theorem and the quantum correlations. As we saw in the previous sections, all quantum correlations are inevitable consequences of the parallelizability of the 7-sphere, which in turn is a consequence of Hurwitz’s theorem. So the innocent looking algebraic equality (2) has far reaching consequences, not only for the entire edifice of mathematics, but also for that of quantum physics:

Home page

Leave a Reply Cancel reply

Recent Posts

Recent Comments

Archives

Categories

Meta