Click here for my Challenge to Bell’s Theorem.
Why have the Bell mafia stooped to playing dirty politics?.. To suppress this stark evidence,
and to deny the inconvenient truth presented in these published papers.
Since March 2007 I have repeatedly shown—in many different ways—that the strong quantum correlations we observe in Nature are natural consequences of the topological properties of the physical space itself. They have nothing to do with quantum entanglement or non-locality per se. Just as gravitational effects were shown by Einstein to be due to the geometrical properties of spacetime, I have shown that quantum correlations are due to the spinorial properties of spacetime. Once the correct topology of spacetime is taken into account, it is trivial to reproduce the EPR-Bohm correlation in a complete, local, realistic, and deterministic manner. This of course amounts to a decisive refutation of Bell’s so-called “theorem”, which you can find on the next page. A succinct summary of my local model for the EPR-Bohm correlation can be found here. One of the most accurate event-by-event numerical simulations of my local model for the EPR-Bohm correlation can be found here.
If you are familiar with my argument against Bell’s theorem and looking for further consolidations of my disproof, then the page that might interest you is this one: Origins of Quantum Correlations. Or perhaps you are an experimentalist. Then you may find this page interesting: Proposed Macroscopic Test. Finally, there is this page about the Topologies of the 3- and 7-spheres, which might interest you if you are more topologically inclined.
If you are interested in event-by-event simulations of my local model, then you may find them discussed in this paper. At least five explicit, event-by-event, numerical simulations of my local model for the EPR-Bohm correlation have been independently produced by five different authors, with codes written in Java, Python, Mathematica, Excel VB, and “R“. The above 2D-surface version of the simulation of my local model can be found here. I discuss two of these simulations in the appendix of this paper. A compact translation of one of these simulations (from Python to Mathematica) can be found here. Each simulation has given different statistical, geometrical, and topological insights into how my local-realistic framework works, and indeed how Nature herself works. A real-time demonstration of one of the main simulations which runs locally in any web browser can be found here and here. It starts to run immediately on loading and takes a minute or two to calculate 10 million trials.
In addition to these simulations, I have recently won the 10,000 Euros offered by Richard Gill for theoretically producing the 2n angular momentum vectors, 
![\displaystyle {\cal E}({\bf a},\,{\bf b})\,=\lim_{\,n\,\gg\,1}\!\left[\frac{1}{n}\!\sum_{k\,=\,1}^{n} \{{sign}\,(+{\bf s}^k\cdot{\bf a})\}\, \{{sign}\,(-{\bf s}^k\cdot{\bf b})\}\right]\,=\,-{\bf a}\cdot{\bf b}\,, \ \ \ \ \ \ \ (2)](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%7B%5Ccal+E%7D%28%7B%5Cbf+a%7D%2C%5C%2C%7B%5Cbf+b%7D%29%5C%2C%3D%5Clim_%7B%5C%2Cn%5C%2C%5Cgg%5C%2C1%7D%5C%21%5Cleft%5B%5Cfrac%7B1%7D%7Bn%7D%5C%21%5Csum_%7Bk%5C%2C%3D%5C%2C1%7D%5E%7Bn%7D+%5C%7B%7Bsign%7D%5C%2C%28%2B%7B%5Cbf+s%7D%5Ek%5Ccdot%7B%5Cbf+a%7D%29%5C%7D%5C%2C+%5C%7B%7Bsign%7D%5C%2C%28-%7B%5Cbf+s%7D%5Ek%5Ccdot%7B%5Cbf+b%7D%29%5C%7D%5Cright%5D%5C%2C%3D%5C%2C-%7B%5Cbf+a%7D%5Ccdot%7B%5Cbf+b%7D%5C%2C%2C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%282%29&bg=ffffff&fg=000000&s=0 "\displaystyle {\cal E}({\bf a},\,{\bf b})\,=\lim_{\,n\,\gg\,1}\!\left[\frac{1}{n}\!\sum_{k\,=\,1}^{n} \{{sign}\,(+{\bf s}^k\cdot{\bf a})\}\, \{{sign}\,(-{\bf s}^k\cdot{\bf b})\}\right]\,=\,-{\bf a}\cdot{\bf b}\,, \ \ \ \ \ \ \ (2)")
together with
![\displaystyle \lim_{\,n\,\gg\,1}\!\left[\frac{1}{n}\!\sum_{k\,=\,1}^{n} \{{sign}\,(+{\bf s}^k\cdot{\bf a})\}\right]=\,0\,=\lim_{\,n\,\gg\,1}\!\left[\frac{1}{n}\!\sum_{k\,=\,1}^{n} \{{sign}\,(-{\bf s}^k\cdot{\bf b})\}\right]\!, \ \ \ \ \ \ \ (3)](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Clim_%7B%5C%2Cn%5C%2C%5Cgg%5C%2C1%7D%5C%21%5Cleft%5B%5Cfrac%7B1%7D%7Bn%7D%5C%21%5Csum_%7Bk%5C%2C%3D%5C%2C1%7D%5E%7Bn%7D+%5C%7B%7Bsign%7D%5C%2C%28%2B%7B%5Cbf+s%7D%5Ek%5Ccdot%7B%5Cbf+a%7D%29%5C%7D%5Cright%5D%3D%5C%2C0%5C%2C%3D%5Clim_%7B%5C%2Cn%5C%2C%5Cgg%5C%2C1%7D%5C%21%5Cleft%5B%5Cfrac%7B1%7D%7Bn%7D%5C%21%5Csum_%7Bk%5C%2C%3D%5C%2C1%7D%5E%7Bn%7D+%5C%7B%7Bsign%7D%5C%2C%28-%7B%5Cbf+s%7D%5Ek%5Ccdot%7B%5Cbf+b%7D%29%5C%7D%5Cright%5D%5C%21%2C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%283%29&bg=ffffff&fg=000000&s=0 "\displaystyle \lim_{\,n\,\gg\,1}\!\left[\frac{1}{n}\!\sum_{k\,=\,1}^{n} \{{sign}\,(+{\bf s}^k\cdot{\bf a})\}\right]=\,0\,=\lim_{\,n\,\gg\,1}\!\left[\frac{1}{n}\!\sum_{k\,=\,1}^{n} \{{sign}\,(-{\bf s}^k\cdot{\bf b})\}\right]\!, \ \ \ \ \ \ \ (3)")
where n is the number of experiments performed. These results strongly suggest that my proposed experiment will be a spectacular success. It will reproduce the manifestly local-realistic and yet strong correlations exactly as I have predicted in my papers, confirming my hypothesis that physical space we live in respects the geometry and topology of 
Here is a quote from John Bell, which may inspire you to explore these pages further:
“Now nobody knows just where the boundary between the classical and quantum domain is situated. … A possibility is that we will find exactly where the boundary lies. More plausible to me is that we will find that there is no boundary. It is hard for me to envisage intelligible discourse about a world with no classical part – no base of given events, be they only mental events in a single consciousness, to be correlated. On the other hand, it is easy to imagine that the classical domain could be extended to cover the whole. The wave functions would prove to be a provisional or incomplete description of the quantum-mechanical part, of which an objective account would become possible. It is this possibility, of a homogeneous account of the world, which is for me the chief motivation of the study of the so-called “hidden variable” possibility.” (From Chapter 4 of Bell’s book, Speakable and Unspeakable in Quantum Mechanics.)
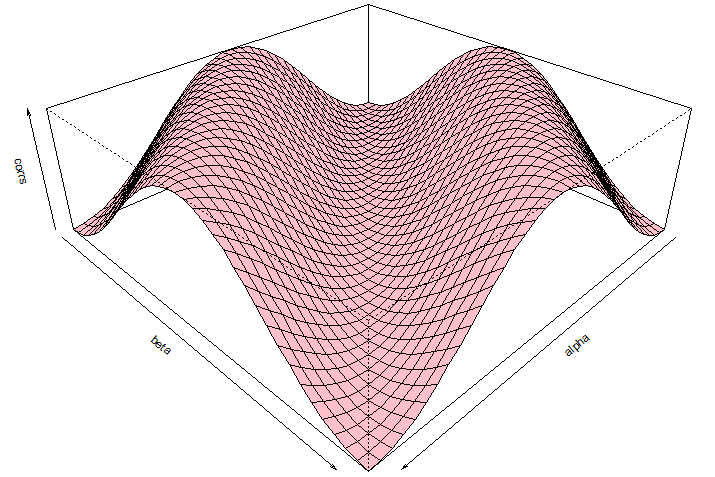
These plots illustrate the role played by the topology of
This confirms that Bell’s theorem stems from topologically naïve assumptions!
It is important to note that I have systematically debunked all of the misguided claims made against my local realistic framework by certain uninformed and unqualified individuals.
More specifically, equations (1.22) to (1.26) on page 10 of my book, as well as similar set of equations in this paper, have been explicitly verified (in great detail) by Lucien Hardy, among several other high profile and exceptionally competent physicists and mathematicians around the world. In fact, any competent reader with only basic skills in mathematics should be able to reproduce equations (1.22) to (1.26) of my book rather effortlessly:
where Einstein’s summation convention on the tensor indices is implicit. The notation and meaning of these equations are also explained in great detail in this paper and in this preprint. The equations have also been verified numerically in the GAViewer (which is a computing implementation of Geometric Algebra) by Albert Jan Wonnink, in these two fine simulations.
All of the so-called arguments against my disproof to date are based on an elementary logical fallacy—the Straw-man Fallacy. What the critics do is deceitfully replace my model X with its grossly distorted misrepresentation Y, and then pretend—by refuting their own distortion Y (by resorting to deliberate dishonesty, wilful deception, or out of sheer incompetence)—that they have undermined my actual model X. Such a dishonest strategy is an insult to the scientific process (for more details, see, for example, these papers). Worse still, when their dishonest strategy is exposed, some critics (e.g. Richard Gill) stoop to dirty political tactics and criminal activities instead of admitting their incompetence in physics and mathematics.
Unlike Bell himself, some of the followers of Bell are naïve, uninformed, and dishonest. The goal of such Bell mafia has been to target my academic affiliations using dirty tricks in order to debilitate me financially and prevent me from publishing my results. Richard Gill, for example, has been writing malicious letters to anyone and any institution connected to me or my work on Bell’s theorem to discredit my work and debilitate me financially, so that I can no longer publish my results with scientific credibility. Hopefully vicious personal attacks, verbal abuse, smear, online harassment, intimidation, and writing malicious letters to my academic superiors by the Bell extremists like Richard Gill will not distract us from the scientific truth. It is disappointing that some unscrupulous members of the “foundations” community condone such despicable tactics by the likes of Richard Gill and Scott Aaronson.
More recently a number of sociologists of science have identified some of the critiques of my work as a form of scientific misconduct. For example in this analysis the author identifies the main culprit as pseudoskepticism: “uttering negative conclusions about someone else’s work that are downright false.” Science is paying a very heavy price for this form of misconduct.
Should the community ignore the crimes committed by Richard Gill and Scott Aaronson? Both of these individuals have used all sorts of dirty political tactics to hurt me academically and financially. I therefore call upon the scientific community to have their professorships revoked when my proposed experiment finally vindicates my refutation of Bell’s theorem.
So far the establishment has been protecting these criminals and punishing their victims.
In my view, those individuals and academic institutions who have condoned the contemptible actions by the rogues like Scott Aaronson and Richard Gill are equally guilty.
PS: There are other physicists who have also noted that the Bell militants, like Richard Gill, “continue to obstruct and intimidate, by astroturfing, [cyber-bullying], writing threatening letters to bosses, employers, journal editors, etc., to suppress the truth from coming out. Those who have staked their whole careers on [quantum] mysticism, or have financial interests in it [such as Scott Aaronson], feel threatened by the truth and lash out at critics.”
PPS: It is also worth noting that Richard Gill has been banned from Paul Snively’s blog, Fred Diether’s science forum, Wikipedia, and several other Internet sites (including this blog) for lying compulsively, spamming, and other menacing, unruly, and unethical behaviour. He has a nasty habit of spamming every Internet venue with blatant lies and malicious smears about anyone whose work he perceives to be a threat to his vested interests and dogmatic beliefs. His latest attempt of bogusly criticizing my work was rejected even by the arXiv moderators. Unfortunately most unsuspecting scientists are unaware that Gill is a scoundrel and a thief.
PPPS: Richard Gill pretends to be upset with me because he thinks that I call him a “morally bankrupt, algebraically challenged, third-rate statistician.” He fears that I have exposed him to be a compulsive liar, and dreads that perhaps I also suspect him to be a certified sociopath.
An update: On Valentine’s day 2015 I resigned from the Foundational Questions Institute (FQXi). I am reproducing my resignation letter below. The trigger for my resignation was the fact that FQXi offered a membership to Richard Gill despite having witnessed how he harassed and bullied me online on their own website. To be fair to FQXi, they are unaware of the duplicitous character of Richard Gill. They are unaware of the dirty tricks and malicious underhand tactics Gill has been employing behind the scenes to undermine my academic credibility. As noted above, he has been systematically targeting my academic affiliations from the beginning of his malicious campaign against me. So things had been building up for a long time, on several fronts, within FQXi as well as within Oxford University. Offering Gill a membership of FQXi was the last straw. If my resignation letter seem strongly worded to you, then you are probably unaware of what has been going on for the past several years:
Meanwhile, the relentless campaign of petty harassments by Richard Gill continue unabated.
Ask Karl Hess, ask Michel Fodje. I am not the only victim of criminal harassment by Richaed Gill.
And I am not the only one who has been lynch-mobbed online by Scott Aaronson.
After many years of relentless harassment, Richard D. Gill has finally shown some remorse and regret publicly, at this public forum, for his obsessive, compulsive, psychopathic actions. In a private email to me, Fred Diether and Jay R. Yablon, he has also admitted that he tried to destroy my academic career systematically, “by pulling strings in high places.” For example, during 2012 and 2014 Richard Gill sent a series of malicious letters about me to the President of my College at the University of Oxford, with the aim to debilitate me both academically and financially, so that I could not continue my research challenging Bell’s theorem.
Just one individual (Richard D. Gill) has started ten threads on PubPeer over the past nine years attacking eight of my papers on Bell’s theorem. The same individual has tried to have all of my papers stonewalled and/or retracted from jorunals over the past nine years. The same individual has written a series of malicious letters about me to the President of my College at Oxford University since 2011. The same individual has admitted that they “…should not have pursued [me], like [they] did, to all far corners of the internet! It was an unhealthy obsession on [their] part, and it caused harm to [me] and to others, which [they are] deeply sorry for.” That is not a normal behavior of any human being, let alone a retired university professor.
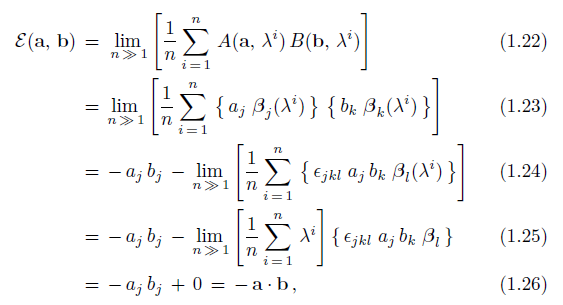
Hi Joy,
Like the blog name!
You have been bookmarked.
Rick
Thanks, Rick.
I hope to see you here often.
Joy
A great start Joy!
The best of luck.
Jonathan
Hi Joy,
Good to see you’re still pushing back!
Best,
Ed
Thank you, Edwin and Jonathan.
And welcome to my blog!
Best,
Joy
I was wondering where the discussion could continue after it was stopped at FQXi. Good to see this blog!
Albert Jan
Thank you, Albert Jan.
Welcome to my blog!
Best,
Joy
Hi Joy,
What is really amazing is that it took so long for someone to properly figure this (quantum correlations) out since 1964. Perhaps people just want quantum mechanics to remain mysterious. And… probably a lot of smart talent got diverted by superstring theory.
I know you did your first paper in 2007 but did you have some notion of maybe how to solve this before then? Any pre-2007 history you would like to mention?
Best,
Fred
Hi Fred,
Thank you for your question. No, prior to 2007 I did not have any notion, or even inclination, to understand quantum correlations local-realistically. As a former Ph.D. student of Abner Shimony I implicitly accepted Bell’s argument. When I was his student Abner was the ultimate authority on the subject. He seemed to have thought about it from every conceivable angle. He had an answer for any possible question one could have about it. So it did not occur to me that there could be anything wrong with Bell’s argument because I trusted Abner’s judgement on it. Besides, Bell’s argument is so deceptively simple. How could it possibly be wrong? So I accepted Bell’s theorem as something one has to live with. Consequently I accepted that quantum correlations are a result of quantum entanglement, and thus accepted non-locality as a fundamental new modality of Nature. In physics we do discover new aspects of Nature time and again, so it is not hard for most students to accept counterintuitive things like non-locality. The real problem for me back then was to reconcile entanglement with the general covariance of general relativity, which is an intrinsically local theory. So that is what I was trying to do at Perimeter Institute until the end of 2006. But towards the end of that year I spotted an error in the very first equation of Bell’s paper (as I discuss on the next page). The rest is history, as they say.
Best,
Joy
Joy,
Beautifully stated. Thanks for the insight.
Tom
Hi Joy,
While researching more about macroscopic “entanglement”, I ran across this paper,
http://arxiv.org/abs/1203.0033
“Solving the Quantum Nonlocality Enigma by Weyl’s Conformal Geometrodynamics”
and am wondering if there might be a connection between Weyl’s curvature described in the paper and torsion of the parallelized 3-sphere? Also, I am not quite sure what they are considering to be the hidden variable(s). De Martini is also involved in a paper that may be relevant to the macroscopic experiment that I was describing on your experiment page. But I will wait to post comments about that as I am still digesting the paper more thoroughly as it is heavy into experimental lingo.
http://arxiv.org/abs/1202.5518
Best,
Fred
Hi Fred,
Thanks for these papers by De Martini’s group. I had a brief look at them, but I don’t see any obvious connection between their Weyl curvature and my torsion within a parallelized 3-sphere. I am also unsure about what they are considering as hidden variables. It seems to me that they are swapping non-locality with some equally dubious ideas. In any case, their idea is conceptually and mathematically not as clear-cut as my torsion hypothesis.
Best,
Joy
Joy,
Great work. But most work simply accepted and absorbed into mainstream science is normally not ‘great’ by definition, so it seems having a cross to bear and being stoned may be the essential price to pay for ultimate greatness! You seem to have noted my comments about not over reacting, or perhaps have just become more sanguine. What doesn’t kill us makes us stronger.
But of course I would support your findings as, despite your doubts, I think I have now shown I arrived at the same place via a wholly different ontological pathway. Indeed I had to reject between ‘mathematical’ cardinalised symbolism and derive nature’s regressive uncertainty to get there. I think finding that place by two such different routes is a massive testament that it’s the right place. I you haven’t yet read my 2013 essay by now (2nd in the community scoring) I hope you will and will comment. Helicity and the quantum mechanism underlying Malus’ Law are the keys. I must confess I can’t decode your maths, but I’m now certain I’m in the same place as you.
An important finding referred there is my prediction of orbital asymmetries in experiments a la Aspect with time resolved single photon correlations. A search turned up that very prediction hidden in Aspects discarded data in the French version of his thesis. The vast majority of the data was discarded as he could find no theoretical explanation at the time!. See also the links in the first blog under the abstract. I provide a link to an analysis by Caroline Thompson, now deceased I understand, who also found that data. Alain Aspect has not replied to my letter!
I hope you may now form a better understanding of my empirical derivation and its exposure of the flaw in QM. My blog discussions on the APS Linked-in site explain that Bohr did not accept back then that a quantum particle could have any ‘structure’. As soon as we postulate a torus (dipole translating axially to form a helix) which he would now surely accept, the problem is resolved. But I argue Bell was also correct in finding no boundary between QM and SR (we share the quote!) perhaps a better tactic for getting the truth ‘seen’?
Very best wishes
Peter
All is well, now that a ‘man of controversy’, Joy Christian, is back at Wolfson College, Oxford.
His recent papers have been the target of unabashed & unreasoned politics on the physics blogosphere. Joy’s most recent paper is crystal clear:
http://arxiv.org/pdf/1301.1653.pdf
In physics, framing one’s papers in a ontic context; let alone refutation often can buoy an attack.
In supporting an Über ansatz – it is often better to assemble a battalion – than going solo on a paper. He went alone.
All ‘block & no tackle’ – Joy set sail on this course several years ago.
Joy Christian obtained his Ph.D., in Foundations of Quantum Theory, under the supervision of the renowned philosopher and physicist Professor Abner Shimony.
A decade later, his paper, “Disproof of Bell’s Theorem”, would incite a war.
Many refuters admitted to having not read his papers, book, or supporting references.
Joy Christian’s recent publication consolidating papers over the last decade.
I was left to think that few know Clifford Algebra and Algebraic Topology; in context.
This is a maelstrom in a teapot controversy of our day.
Tea is being served on both sides.
J. Christian was not entirely alone.
Generalization of the Bloch sphere representation of quantum states was, perhaps, first effectively posited by Prof. Remy Mosseri of Universites Pierre et Marie Curie.
R. Mosseri relevant papers start at around 2001**.
J. Christian and R. Mosseri are largely consistent in approach in Generalization of the Bloch sphere – J. Christian extends an ontic context.
Quoting Abner Shimony on underdeterminism of nonlocality – refering to Fine in a paper (Fine 1999)*** :
““That means that the Hardy theorem, like other variants on Bell, is not a ‘proof of nonlocality’.
It is a proof that locality cannot be married to the assignment of determinate values in the recommended way – That is interesting and significant.
It is not, however, a demonstration that quantum mechanics is nonlocal, much less (as some proclaim) that nature is.” – Fine’s analysis of Hardy’s construction relies upon his earlier paper (Fine 1982b)””
**Refs:
R. Mosseri and J. Christian citations, as reference, inclusing the seminal, ‘Geometry of entangled states, Bloch spheres and Hopf fibrations’ by R. Mosseri:
http://arxiv.org/find/all/1/au:+Christian_Joy/0/1/0/all/0/1
http://arxiv.org/abs/quant-ph/0108137
http://arxiv.org/pdf/quant-ph/0310053
http://www.brownwalker.com/book.php?method=ISBN&book=1599425645
*** from a Plato post at Stanford’s SEP
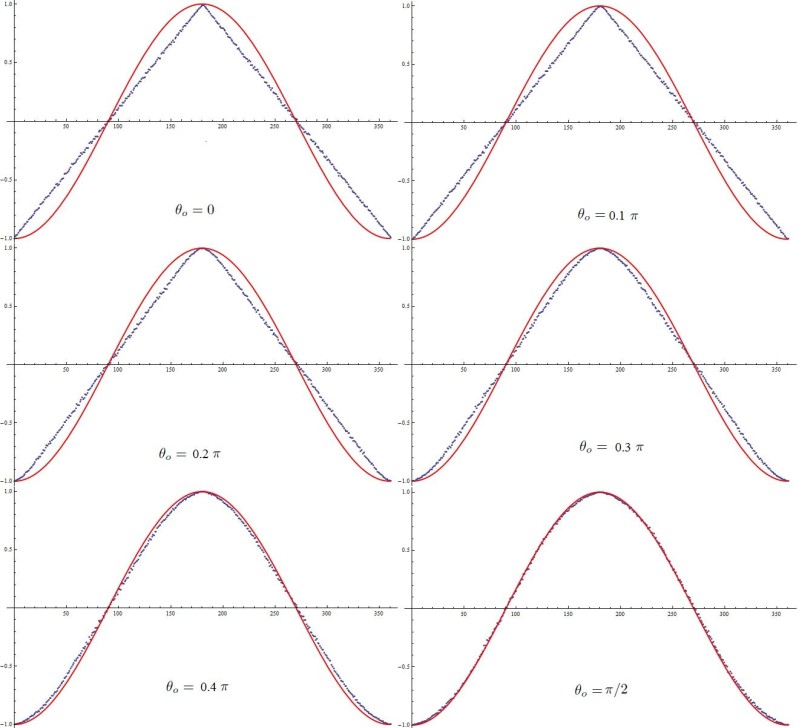
I am grateful to one of my former tormentors, Richard Gill, for reproducing yet another simulation of my 3-sphere model for the EPR-Bohm correlation. It is good to see my local model being confirmed in so many different simulations, especially because many critics of my work had previously misinterpreted my one-page paper and claimed that my model predicts constant correlation, namely -1, for all values of the experimental parameters a and b. The recent plethora of simulations confirming my local model clearly show that the critics (which included Richard Gill, Scott Aaronson, James Weatherall, Adrian Kent, Lucien Hardy, an exquisitely qualified panellist recruited by FQXi to evaluate my work, a distinguished board member of Physical Review D, numerous referees and editors of many established journals, as well as some lesser known critics) were grossly mistaken. So by taking a U-turn Richard Gill has now done a great service to physics by reproducing some of the simulations of my analytical local model in a different programming language.
Having said that, it is very important to remember that the numerical simulations by themselves are not the actual model. They only provide confirmation of the exact analytical model, which is summarized in eight elementary equations in these two pages. After all, Bell’s analytical claim was hardly about numerical simulations.
Thanks for your great work. I appreciated it a lot, even if I’don’t feel not very comfortable whith the mathematical you use (well, ignorant).
I was asking me some questions, maybe silly, and in a bad english (I’m french) :
Is the S3 topology a consequence of superposing by the thought what happened at each Polarisor in a S2 topology, but oriented differently ?
If Alice and Bob are looking at a rotating disk between them, they will see opposite rotation. Is there an analogie with Alice and Bob looking at this unique rotating disk and the appartus looking at the same ray of light ?
If so, to compare what see Alice and Bob on their own S2 sphere, is it necessary to surimposed this 2 spheres, but of course inversing orientation of one of them, since there looking at the very same objet but from the opposite point of view, leading to an S3 sphere ?
- General relativity may live in reality in our common 3d euclidean space
(making some consequences like absolute time etc…)
- General relativity may be a manifestation of quantum consequences.
Ex. Higgs boson density is general relativity curvature. Mass is the local transformation of Higgs bosons to other particles like virtual photons. Creating different Higgs pressures, hence gravity same way GR describes. Time is background Higgs boson density.
- No action at a distance. Entangled form beginning.
- Wave duality. Particle simply create a wave on Higgs field (or Bosons) while surfing it. Explaining double split and else like pilot waves.
- Reformulate QCD in euclidean? Explains confinement.
I am not a mathematician. Not even a physicist, so…
Hello,
Maybe will you be interested by a non violation of Bell’s inequality demonstration:
http://dx.doi.org/10.4236/jmp.2014.514137
Best wishes
Dr. Christian,
First, thank you for your exhaustive—and apparently exhausting—work. I happened upon it some weeks ago, and was particularly struck by your Response #4 in your Replies to Critics, because of its clarity in exposing the assumption of scalar algebra and its motivation—which shouldn’t be necessary in the 21st century—of adopting at least Hamilton’s 19th-century quaternionic algebra if not Clifford’s full geometric algebra in order to avoid singularities.
Because I come to the subject from the perspective of “theoretical” computer science, I decided to connect the dots in my own blog post, which elaborates why mathematical singularities are fatal to logical proof via this detour through computer science. I hope you find it some measure as engaging as I find your papers.
Hello Paul,
Thank you for your message, and for the link to your very nice blog post about my work. In fact I had noticed your post a few days ago and was thinking about dropping you a line. I refrained from doing so, because I didn’t want to flood your blog with hostile and impolite reactions. Wherever I show up on the internet these days, hostility and aggression seem to follow.
I had forgotten about my Response #4, since so much has happened since 2007. But reflecting back on it — especially after reading your blog post — brings back some bittersweet memories.
In your comments I particularly like the connection you have made: algebra with operations lacking the closure property -> mathematical singularities -> partial functions -> logical inconsistency. This sequence really makes the logic crystal clear. The rest are details, as Einstein would have put it. But we physicists tend to get hung up on details, and hence all the extensive elaborations on my blog and in my publications.
Thank you again for your incisive input, and please keep in touch.
Best,
Joy
I was really impressed with what I read of your work in New Scientist, and was looking forward to it changing things a lot. I’m an embedded systems engineer, though I did take a little QM at uni. I reached the point where I could almost understand Bells work, but never really got to grips with it.
I always took Einsteins view, I just can’t accept non-locality. Not that I’m qualified to have an opinion on that.
You know this already, but I’ll say it anyway: You’ve disproved THE PREVALENT INTERPRETATION of Bell’s theorem. Bell’s own interpretation, which I am sure you’ve read, “… what is proved by the impossibility proofs is lack of imagination.” (Bell)
I am sure Bell would be one of your foremost proponents if he was alive today. [From https://en.wikipedia.org/wiki/Bell%27s_theorem
… Bell’s deliberate effort to encourage and bring legitimacy to work on the completeness issues, which had fallen into disrepute. Later in his life, Bell expressed his hope that such work would “continue to inspire those who suspect that what is proved by the impossibility proofs is lack of imagination.”
A quote I have seen which seems to originate with Max Planck, makes me think Planck may well have been familiar with what you have to put up with:
“A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die, and a new generation grows up that is familiar with it.” I read somewhere that the entire classical physics old guard had to die off before the new quantum physics could flourish, arround 1900. How much more inertia must there be now, post 2000, that you have to waste your time and energy on. The physics community now must be thousands of times bigger than it was then.
I am disapointed that science has come to this, but it is probably inevitable given human nature. On the plus side, maybe you’ll reply to my email, maybe meet over a few beers someday. Being close to oxford and cambridge is one of the few things I like about the UK. So consider this fan mail, and have a fine day.
I was wondering if your work could be relevant to quantum computation. I bring it up because if the ‘magic’ in QC is not based on non-locality, what IS it based on? I think there is a computational side which everybody seems to be blinded by non-locality to:
1. The language of physical reality is PDE’s, for example Schrodingers equations.
2. There is no proof that in general PDEs can be modelled efficiently on a classical computer. And I’m going to assert that in the general case, efficiently simulating a PDE is (presently) at least as difficult as the integer factorisation problem. Evidence being that at present all attempts to simulate a quantum processor on a classical platform takes time exponential on the number of qbits. Computationally infeasible.
I appreciate that is not a proof. But I think is it a reasonable summary of the current position, with non-locality removed from the arguments.
Do you think that an analog processor could be built to model the equations in a quantum processor? It would have to use analog elements which emulate the algebra’s you describe in your work, but there’s no magic in that.
There are some proofs arround which show that NP-complete problems can be solved in polynomial time if the right kind of non-linearities are introduced. That might be possible too.
Maybe analog computers return.
Would love to hear your take on those thoughts.
Hello Lance,
Thank you for your kind comments.
You are quite right to note that “Bell would be one of [my] foremost proponents if he was alive today.” He certainly would have been. I know this because I have been privileged enough to have met Bell and discuss physics with him on several occasions, here in Europe and in the United States where I was a PhD student of Abner Shimony (the “S” in the Bell-CHSH inequality). Unlike some of his lesser followers, Bell was quite open minded about his own theorem. At least he would have listened to what I have to say rather than attack me dogmatically.
As for your questions about quantum computers, not being an expert on the subject I can only make some very general remarks. Scalable quantum computers will almost certainly require quantum entanglement. But my work shows that quantum entanglement is not a fundamental feature of the world. So I am quite certain that scalable quantum computers, exhibiting exponential speed up, are a fantasy. This does not rule out some quasi-quantum like computers. But they will not produce anything like exponential speed up.
My own concern is less about computers and more about the fundamental laws of physics. So my own interest in Bell’s theorem comes from that direction.
Thanks again for your comments.
Best regards,
Joy
Thanks for your reply. I never knew you mixed in such rarefied circles. I admit I had not realised who Abner Shimoni was, my bad.
My maths is far behind me now, and never that strong to boot. Sorry to harp on about the QC bit, bit the next thought is hilarious. I was just reading about the physical experiment to prove your thesis. To my thinking (not to be taken too seriously) (and it looks like there is consensus) there is no need to actually do the physical experiment. An idealised computer simulation, as has been done, should be more than good enough if not better. After all, the whole simulation would be classical mechanics only.
What is implied here is that a quantum computer could be build using a large enough ensemble of squishy rubber balls, appropriately constrained and energised.
Polystyrene beads in a blender?
Excuse my irreverence.
Sorry, I hope I’m not coming across as poking fun. I’m not saying it’s feasible, but that gross oversimplification is not completely unfounded I think.
As a software engineer, I’d love to have a go at a first principles simulation of that. Might be possible to factorise 21 after a few months simulation of rubber balls in an appropriately designed blender.
There are QC simulation codes available out there. I wonder if it would be possible to re-engineer one of those to use qubits built arround a clifford algebra.
Hi Lance,
Your questions are understandable. There are several different issues to consider here.
First, some explicit simulations of my model are already done. Here are two examples:
http://rpubs.com/jjc/84238
http://challengingbell.blogspot.co.uk/2015/05/further-numerical-validation-of-joy.html
You may want to check out the blog where the second simulation is discussed. The blogger — Albert Jan Wonnink — has spent much time trying (and succeeding) to simulate my model.
But there is another issue in your questions, which I think is based on a widespread misunderstanding of what the simulations of my model represent. They, or my proposed experiment, have nothing to do with quantum computers. The key idea behind my approach — and this has been misunderstood by nearly everyone — is that the observed strong correlations in Nature are a consequence of the geometrical and topological properties of the physical space itself. This makes the simulations of my proposed experiment rather tricky. For how do you simulate the geometrical and topological properties of the physical space before attempting to simulate the squishy balls experiment within it? This is not an easy question to answer. We may have to do the actual experiment after all to understand the answer chosen by Nature. In this regard I again refer you to Albert Jan Wonnink, who has spent much time thinking about this issue from the perspective of possible simulation on a classical computer.
Best,
Joy
Okay, definitely something there I’m missing.
I did overview the second link you give before I wrote those replies above. Not going to claim to fully understand what was being said. I believe a key issue was how to model a measurement, that gives +/-1 only. I would need to study it a lot more before I have any meaningful questions which weren’t a waste of your time.
My thinking was simply this: A rubber ball, squishy or otherwise is very well defined and understood classically. I could do a finite element simulation from first principles which I am sure would be accurate, no need to invoke your work at all. The key point is that the balls must have structure – spin and alignment have to be taken into account.
My (limited) understanding of Bell’s error is that in the first equation, he attempts to reduce everything down to a scalar, which does not apply in this case.
A detailed first-principles simulation of the double slit experiment should be pretty straightforward. Just energy, momentum, elasticity, losses. A classic finite-elements simulation. Given the nature of the double-slit experiment, it shouldn’t even be that expensive computationally. If spin and alignment are properly taken into account, then an interference pattern must emerge.
That is Bell’s error isn’t it? The classical side statistics he predicts are wrong.
A simulation of the double-slit experiment would be a pretty inarguable demonstration wouldn’t it? That’s possible, surely?
I’m going to go out on a limb and say a desktop PC would be enough for a simulation like that, if it’s theoretically possible.
Excuse my ignorance. I should be talking about one the classic experiments that are meant to demonstrate entanglement, like the quantum eraser experiment or something simpler.
Happier New Year, Joy.
I changed my address after getting unsolicited sales pitches from the Trump org after the election, and decided not to reinitiate an account at FQXi. There is just too much of those whom come there with a personal delusion that they have made a ‘discovery’ that science must accept to save science from itself, when what they have done is to read over their level and come to some psychological construct that puts the contrary and conflicting paradigms of Quantum and Relativistic measurement systems into a bundle that they can believe makes it all make sense. You are quite correct in stating that it is the physical properties which Topological measurement of spacetime properly describes, that accounts for the strong correlations observed in nature. And there-in lies the foundational mathematic treatment to evolve the much sought after Unified Field Theory, and in that unified field globally must emerge the local realistic volumetric determinant of any Unitary Field particle or wave-like projection of raw energy.
Good Luck to you and Fred and Tom, and those other skeptics of the ad hoc Std Model. jrc
Thank you, John.
We will be continuing our work, of course.
Happy New Year to you too!
Joy
Joy,
Though I am still in an early learning stage in Topology, the one thing that helped me most in grasping the inherent mathematical form of your argument came from digesting what you present about the psuedovector in your paper on Macroscopic Observability of Spinoral Sign Changes. And it is in that sign change where Gill and other practitioners of Quantum Spin Mechanics commonly miss the mistake you found in Bell’s opening equation, but which really only displays itself in the end analysis. And that final proof can be found when one reaches the actual transport of R3 into S3 and it becomes apparent that Bell asks us to accept a conjugation of Dot and Cross Product terms to confirm orthogonality between a right hand vector in S3 and a left hand vector in R3 which would place conter-rotating torsion on the axis taken as common to both in the intersection of sets. And that only becomes obvious when one sees that you are correct in pointing out the criterion for completeness must have the form where the transport of terms evolves into R4 which does itself have a time parameter represented as a direction of torsion in S3. I am indebted to Fred for his clarification on chirality, and it may be useful in your presentation to develop that argument of end analysis as an illustration to the newly initiated.
Thanks again for your patience, jrc
Oops,
I should have said “negative polar vector” in referring to the presentation in your paper. Still, this aspect of an implied conjugation is what I had posted in a comment on Jan 10, 2016 @21:11GMT on a FQXi topic#2591 thread of Ian’s 2015 in Review about the Delft experiment. I had been pleased at that time by Tom Ray’s response to that post, and it goes to the Bell enthusiasts claim that a Classical model cannot generate the same n^2 probabilities count as does QM. That claim assumes distribution on an infinite 2D complex plane evolved from the numberline segment of S0; but that could only be true if one ignores that a conjugation across sets in R3 and S3 would necessarily result in eqipartition where half of the sets in R3 would impose a counter-rotating torgue on the common axis, and evolving from S0 into S3 would square the possible probability domain just like QM. There is no boundary between the Quantum and Classical. jrc